The geodesic tortuosity, also called geometric tortuosity, is based on computations of distances/shortest paths through the pore space. Note that there are many definitions of tortuosity, some that are based on computed material properties such as diffusion or electrical conductivity, see the discussion in this paper. The geodesic tortuosity on the other hand is based solely on the geometry of the 3D structure (references listed here).
Definition, geodesic path, direction x, y or z
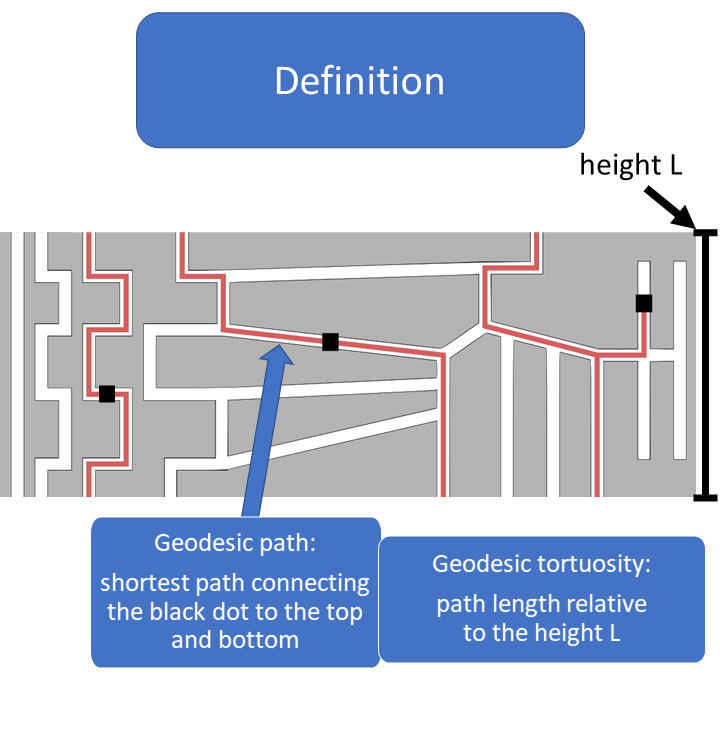
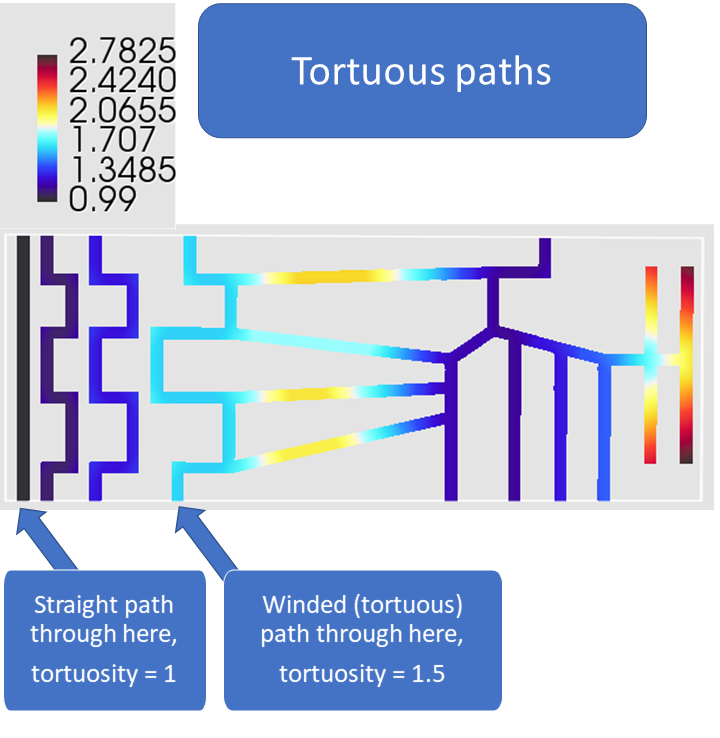
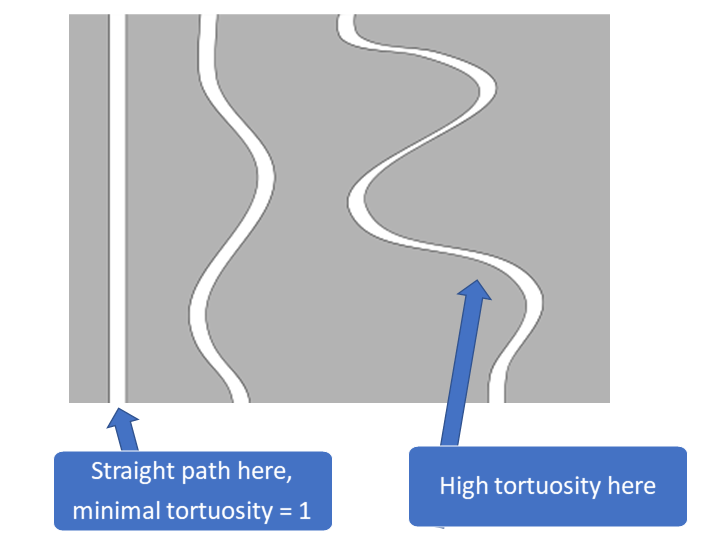
Shortest path through the pore space that connects a voxel (source point) with the two opposite starting faces in a chosen direction (dir. x, y or z).
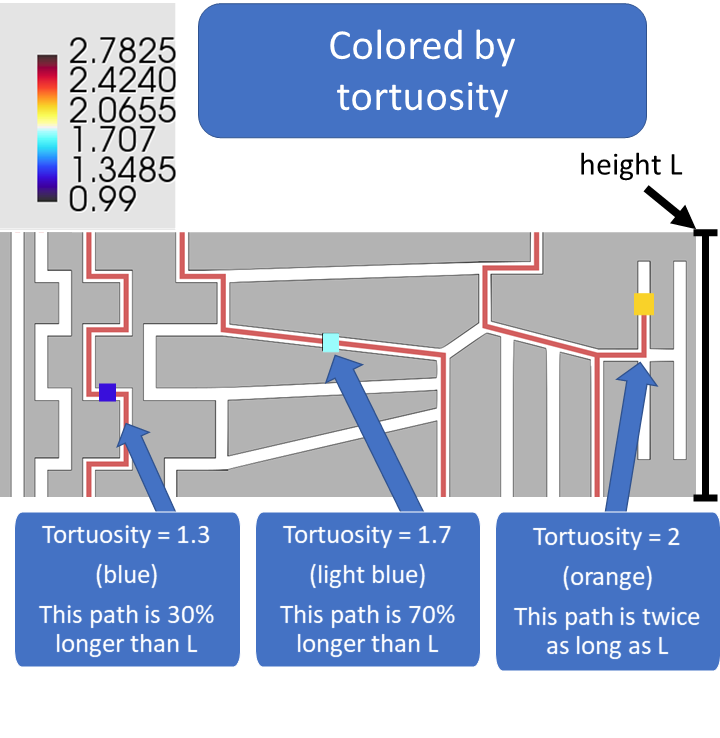
The starting faces that define the geodesic paths are faces of the 3D volume in the chosen direction (top and bottom in the 2D examples below). The starting faces can be visualized in Mist, see the video below. The geodesic tortuosity is defined as the relative length of the geodesic path compared to the length of the 3D structure.
Geodesic tortuosity: relative path-length
In Mist
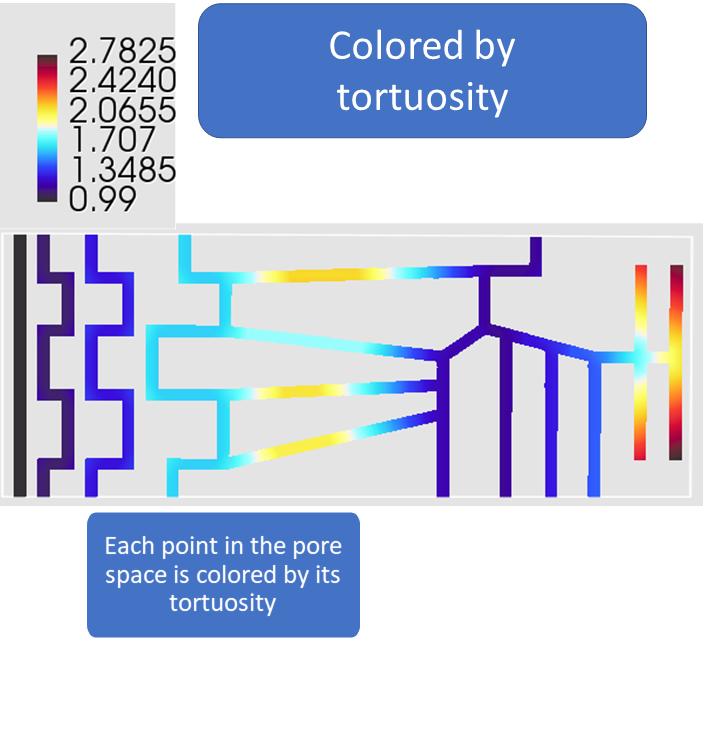
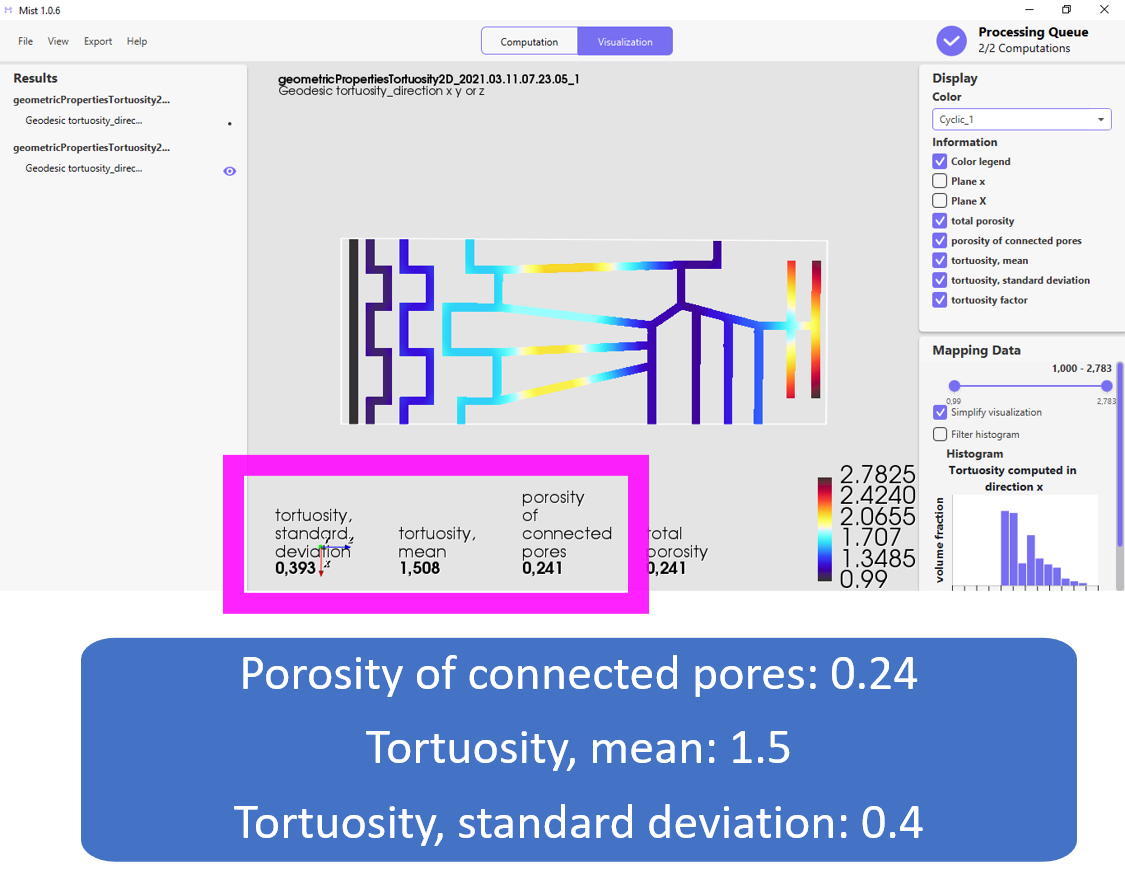
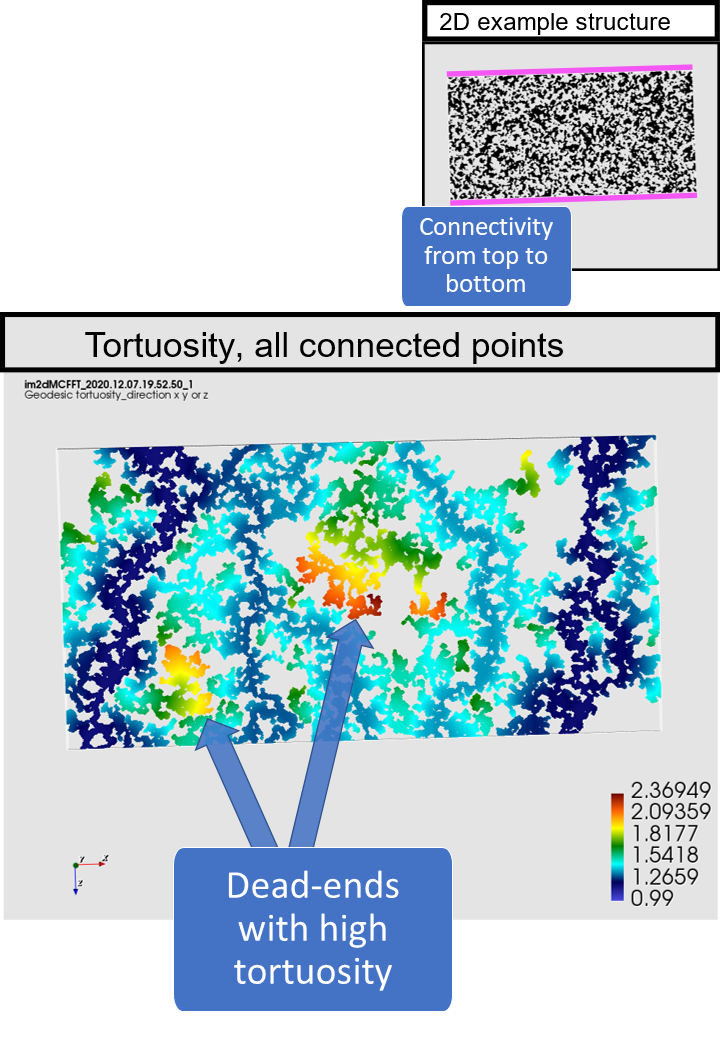
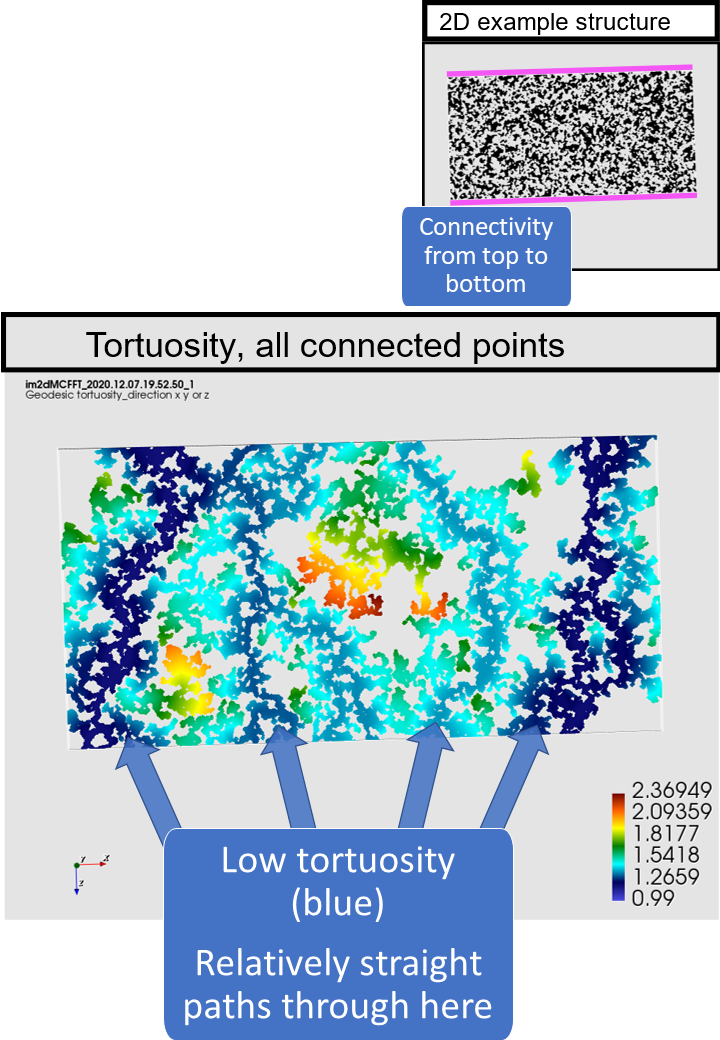
Each pore voxel that is connected to both starting faces in the chosen direction is assigned the value of the geodesic tortuosity. Solid matrix voxels and unconnected pore voxels have value 0.99.
The implementation of geodesic tortuosity in Mist is described in detail in the reference manual (see also Scientific resources).
The geodesic tortuosity has been shown to give good predictions of material properties such as mass transport and electrical conductivity.
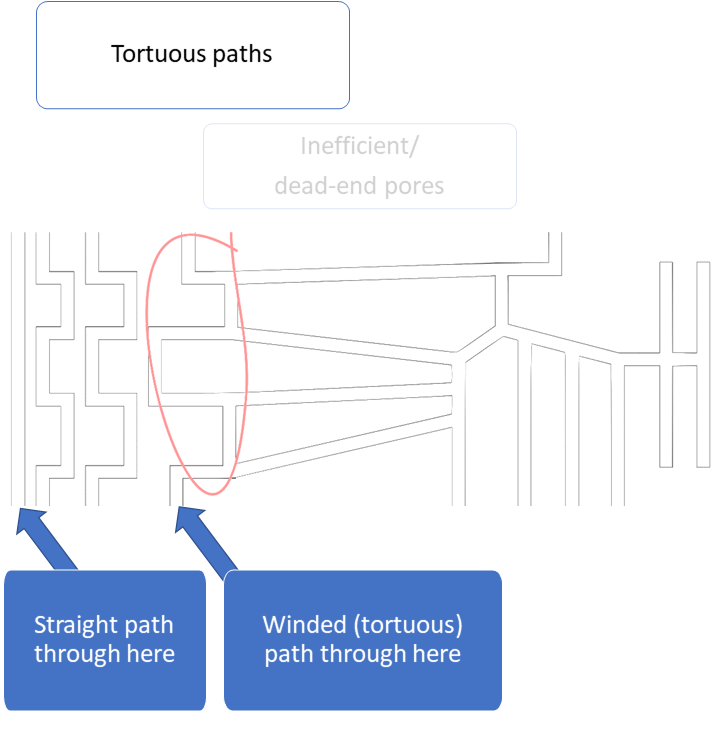
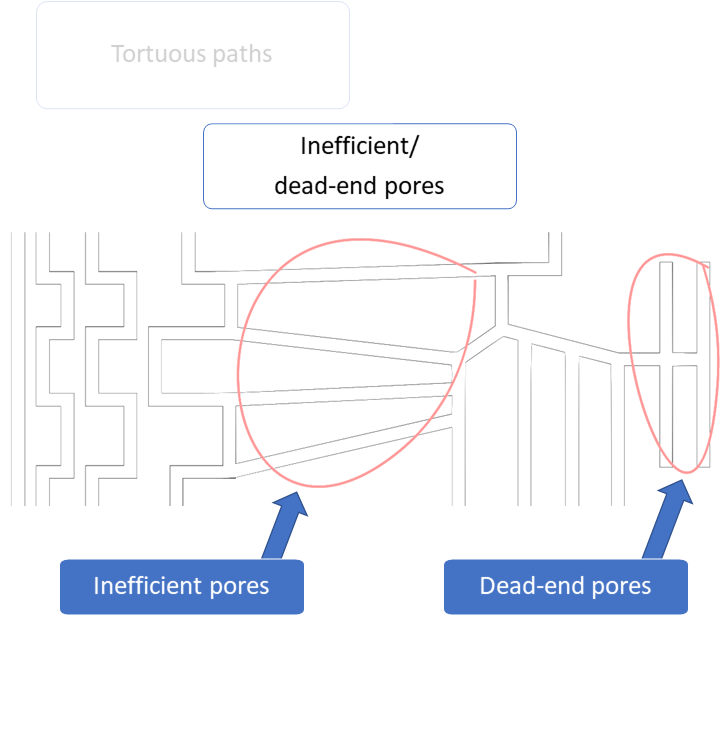
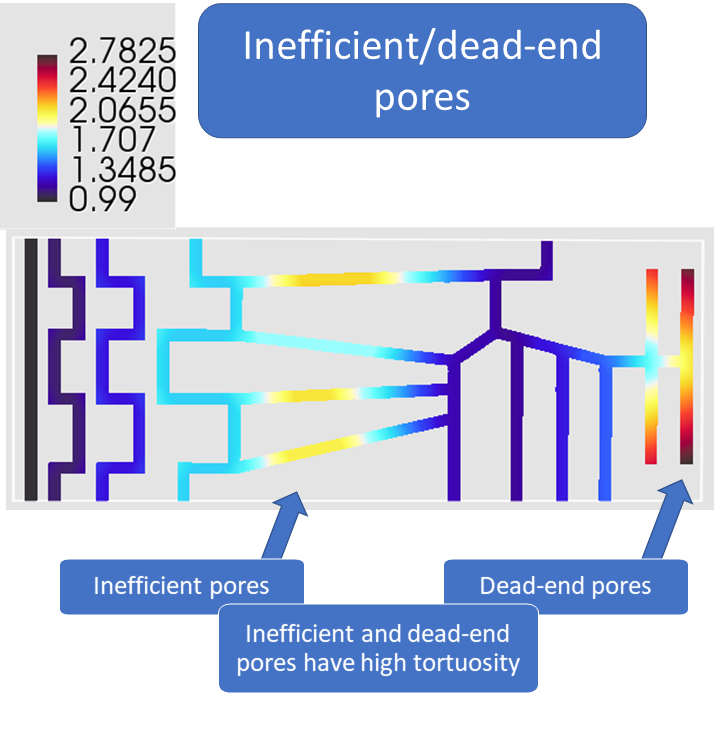
The geodesic tortuosity, or relative path-length, is however often defined only for geodesic paths starting at one of the opposing faces of the 3D volume (inlet tortuosity). The definition of the geodesic tortuosity used in Mist works for all connected pore voxels (full volume tortuosity), see the illustrations in the image slides below. Computing the full volume tortuosity is only twice as computationally demanding as computing the inlet tortuosity, but can give much better predictions of material properties (see Barman et al, 2018). This is mainly because it captures not only tortuous paths but also inefficient/dead-end pores. These connectivity characteristics are illustrated in the image slides below.
For more details about the full volume tortuosity and prediction of material properties using the tortuosity, see these two posts:
Tortuosity illustration
Tortuosity in Mist
How to compute geodesic tortuosity in Mist
(first part of the video)
The video below shows how to compute the geodesic tortuosity in Mist for a demo structure that can be downloaded from here. See also this video from Tutorial, Part I which shows the tortuosity computed in a more complex structure.
Related methods
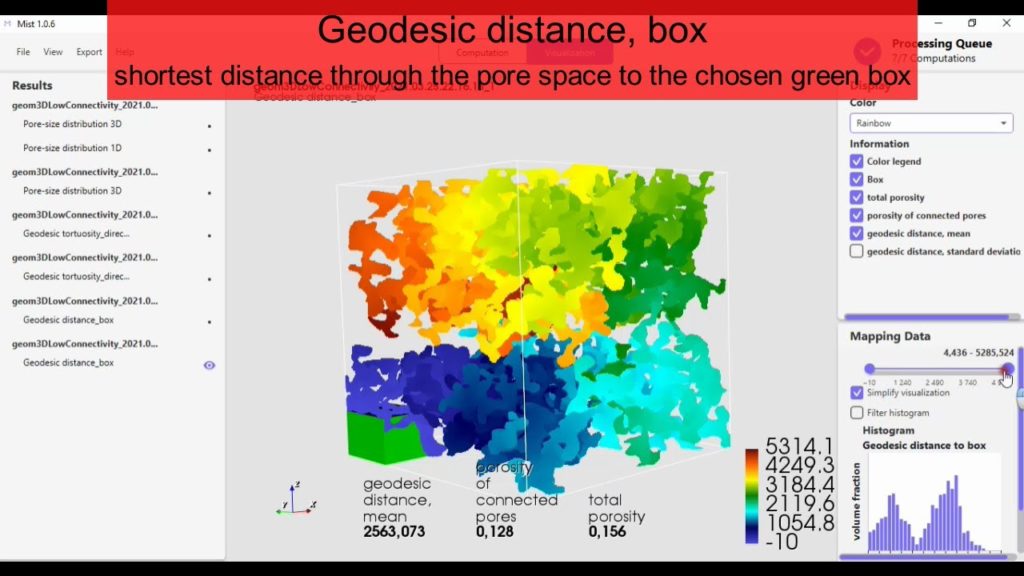
Geodesic distance
Geodesic paths and geodesic channels (advanced methods)